
The x-intercepts of zeroes is where the lines of a parabola crosses the x-intercept. Let us just set them equal to know the relation between the variables. Note that the value of a is the same in both the equations. y=0.Įxample y=2(x-4)^2+8 this equation will then change intoĠ=2(x-4)^2+8 (sub "0" in for the variable "y" ) Let us convert the standard form of a quadratic equation ax 2 + bx + c 0 into the vertex form a (x - h) 2 + k 0 (where (h, k) is the vertex of the quadratic function f(x) a (x - h) 2 + k). To figure out what the "x" intercept is, you would have to subsitute "y" into zero. if The value of "a" is negitive then it would go down. Or even you could think of just by your knowledge if the "a" value is positve then it would open up. you could tell if it opens down or up by A positive "a" draws a smiley, and a negative "a" draws a frowny.

I t also represents whether the quadratic opens up or opens down. The "a" in this equation indicates the stretch/compression (The strtch or compression will multiply the verticle part of the step pattern. The swtich of the signs DO NOT occur to figuring out the "K" value. In the case of figuring out where 'K" goes, you would just have to know that if the value is negative it stay negative and if the number is positive the number will be positve. The resultant equation is the standard form. 1.1.2 Step 2: Simplify the other numbers. 1.1 From vertex to standard form conversion: 1.1.1 Step 1: Simplify the binomial by multiplying by itself. The key information in drawing a parabola is the vertex, which we can read. More specifically, sometimes one version is more appropriate in the real world than another. The "K" in this equation represents the vertical transaltion, so how far up or down the graph is shifted from x=0 Or the orgin. 1 Quadratic equation of parabola: Vertex to Standard form. The factored form of the equation tells us the roots, i.e. It is important to be able to understand both standard and vertex form in order to graph any quadratic equation. Therefore a switch occurs for the signs.Įxample: if the equation is y = 2(x - 4)^2 + 8, the value of h is 4, and k is 8. If "H" is a negative number, therefore the number will be transformed into positive. And the vertex can be found by using the.
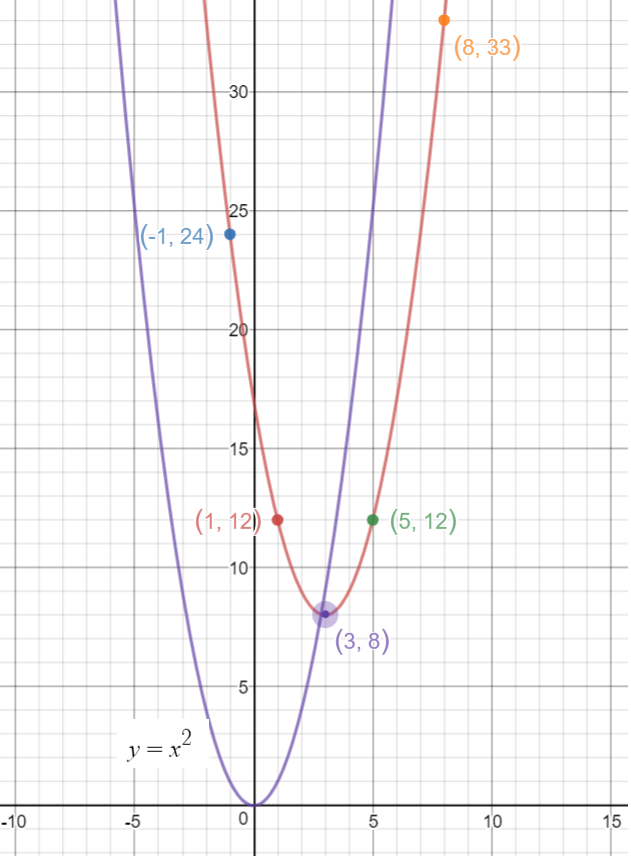
if the Value of 'H" is Positive then the number would be negative. In order to find the vertex of the quadratic equation which is represented as ax2+bx+cy which is the standard form. meaning how far left or how far right the graph is shifted from x=0 also known as the orgin. The "H" in this quadratic equation represents a Horizontal translation. Both the "K" and "H" represent the vertx of the porabala


 0 kommentar(er)
0 kommentar(er)
